Soluzioni degli esercizi capitolo B02
|
|
x |
y |
z |
w |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |

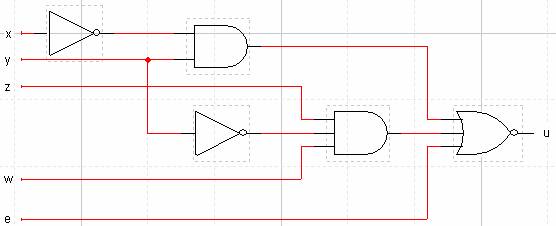
Per mostrare che l’insieme {NOR} è funzionalmente completo basta
dimostrare che con la funzione NOR è possibile realizzare le funzioni NOT, OR, e AND. Sappiamo
infatti che queste ultime tre funzioni costituiscono un insieme
funzionalmente completo.
Ricordiamo la tabella di verità della NOR:
|
a |
b |
a NOR b |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
Dalla NOR
è possibile ottenere la NOT:
NOT(a) = a NOR a
Dalla NOR
è possibile ottenere la OR
a OR b = NOT( a NOR b
)
Dalla NOR
è possible ottenere una AND.
Vediamo come:
Ricordiamo
la prima Legge di De Morgan:
NOT (a AND b) = (NOT
a) OR (NOT b)
Negando
entrambi i membri di questa eguaglianza si ottiene:
a AND b = NOT[ (NOT a) OR (NOT b)
] = (NOT a)
NOR (NOT b)
e quindi otteniamo la AND in termini di NOR e di NOT, che a sua volta
si può ottenere come NOR.
La
funzione ha tre ingessi, a,b ed s, ed una uscita y. Essendo tre gli ingressi, ci
saranno 8=23 differenti combinazioni di ingresso.
I valori dell’uscita y sono assegnati secondo quanto richiesto
nell’esercizio.
|
s |
a |
b |
y |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
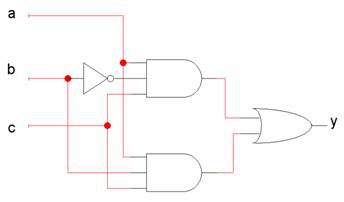
Assegnamo ad y i valori di a quando s=0, ed i valori di b quando s=1.
Dalla
tabella di verità sarà poi possibile ricavare lo schema circuitale che
realizza il sistema richiesto.
L’espressione
algebrica può essere ottenuta come somma (OR) di prodotti (AND).
Nella somma sarà presente un prodotto per ogni ‘1’ che figura nella tabella
di verità sotto l’uscita y. Saranno quindi presenti due prodotti, uno corrispondente alla combinazione di ingressi (a,b,c) =
(1,0,1) ed uno corrispondente a (a,b,c)=(1,1,1) (si tenga presente la tabella
di verità della funzione). In ciascun prodotto, le variabili di ingresso saranno negate se figurano come ‘0’ nella
combinazione in ingresso. L’espressione algebrica così ottenuta sarà quindi
pari a:
y = [a
AND NOT(b) AND c] OR [a AND b AND c]
La
corrispondente realizzazione circuitale si ottiene
immediatamente:
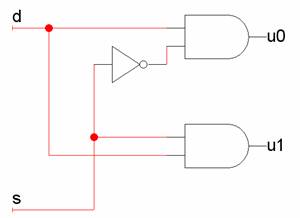
Il componente richiesto dall’esercizio può essere descritto
mediante la seguente tabella di verità:
|
d |
s |
u0 |
u1 |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
Il componente descritto prende il nome di demultiplexer 1-2. Si noti che in questo esercizio veniva chiesto di definire due differenti
funzioni booleane, u0 e u1, tra loro
indipendenti pur avendo gli stessi ingressi. La tabella riportata sopra
rappresenta in realtà due differenti tabelle di verità.